Avaliação de brechas formadas pela ruptura por galgamento de barragens em solo compactado homogêneas através de modelo reduzido

1. INTRODUÇÃO

Estudos de ruptura hipotética (Dam Break) são desenvolvidos para diversos tipos de barragem a fim de se conhecer a mancha de inundação proveniente da falha dessas estruturas. Estes estudos foram foco de diversas pesquisas nas últimas décadas (FROEHLICH, 2008), contudo estes ainda possuem várias incertezas. Estas incertezas provêm, principalmente, do dimensionamento da brecha, da definição do volume armazenado escoado para jusante, da reologia do material armazenado, da determinação do coeficiente de rugosidade do terreno, e da qualidade da topografia disponibilizada. Estudo de ruptura de barragens de rejeito tendem a possuir mais incertezas do que aqueles realizados para barragens de água. Segundo Ribeiro (2015), propriedades geotécnicas e reológicas do rejeito, aspectos geométricos do reservatório e do tipo de maciço da barragem, bem como aspectos hidrológicos-hidráulicos, devem ser levados em consideração, fazendo com que a dinâmica do processo se torne mais complexa.

Diante dessas incertezas, este trabalho busca desenvolver metodologias para a construção de um modelo reduzido de barragem em solo compactado para verificar equações sugeridas na literatura e aplicadas nos estudos de ruptura hipotética de barragens. Dentre as equações matemáticas apresentadas na literatura, estão aquelas aplicadas a fim de determinar os parâmetros da brecha de ruptura. Uma das equações de formação da brecha amplamente utilizada é a equação proposta por Froehlich (2016), contudo, segundo este mesmo autor, as brechas podem ser formadas de várias maneiras e há diversos fatores que podem influenciar a velocidade e extensão de sua formação, tornando difícil modelar a brecha através de equações matemáticas.

 

2. REVISÃO DA LITERATURA

As barragens estão sujeitas a diversos modos de falha sendo os mais comuns galgamento, instabilização do maciço ou fundação, liquefação e erosão interna. Blight (2010 apud ROCHA 2015) apresenta as principais causas de ruptura de barragem de rejeito. Dentre as causas conhecidas, o principal modo de falha é a instabilidade de taludes (22%), seguido de terremoto (17%) e galgamento (16%). Destaca-se que 18% das rupturas analisadas possuem sua causa desconhecida.

Em seu estudo, Davies (2002) calcula a frequência de acidentes envolvendo barragens entre 1970 e 2001. O autor chega ao valor de que, em média, ocorrem de 2 a 5 acidentes por ano o que, em um total de 3.500 barragens, levaria a uma probabilidade de falha anual de 1/700 a 1/1750 por barragem.

Um dos principais modos de falha de barragens é o galgamento ocasionado por um evento de chuva extrema (ICOLD, 2001), o qual proporciona, através da erosão do maciço, a formação de uma brecha pela qual o material contido no reservatório é liberado. Para reduzir o risco de falha de barragens por galgamento, os extravasores das barragens têm sido projetados para critérios cada vez mais rigorosos, tais como ocorrência da Precipitação Máxima Provável (PMP) ou de chuvas decamilenares.

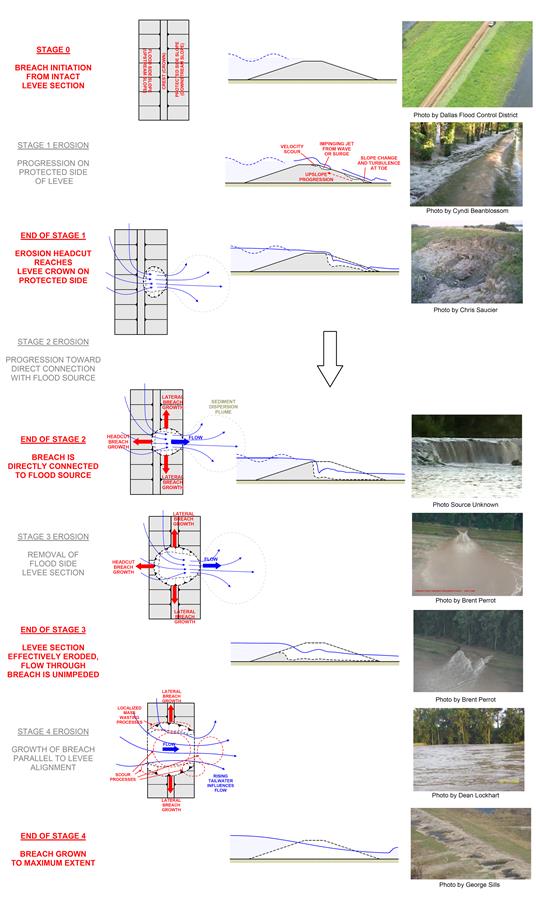
O mecanismo de formação da brecha pode ser dividido em 4 etapas, conforme sugerido por Howard et al. (2009) e apresentado na Figura 2. Na primeira etapa de desenvolvimento da brecha o talude de jusante é erodido de forma regressiva a partir do pé do aterro até o ponto em que esta erosão chega à crista, passando para a etapa 2. Nesta nova etapa a erosão contínua da mesma forma até a brecha estar conectada diretamente com o reservatório. Nestas duas etapas iniciais observa-se que a brecha gera resistência ao fluxo. A partir da etapa 3 esta resistência vai diminuindo até toda seção está erodida, a partir de então inicia-se a etapa 4 onde a brecha cresce apenas lateralmente até sua máxima extensão.

Powledge et al. (1989b), descreveram por meio de experimentos que, para processos de galgamento existem três zonas de erosão, onde atuam dois tipos de regime de escoamento. A primeira zona é a crista da barragem, com escoamento subcrítico e baixa velocidade, declividade e tensões cisalhantes. A segunda zona está a jusante da crista, com aumento da inclinação da linha de energia e erosão na borda a jusante. A terceira zona é o talude de jusante, com aumento progressivo de energia e velocidade até o equilíbrio na perda de energia. O início da erosão ocorre mais frequentemente no pé da barragem e se propaga regressivamente em direção a montante. A Figura 1 exemplifica estas fases.

Figura 1 – Fases e zonas de erosão numa ruptura por galgamento Fonte: Powledge et al., 1989b.

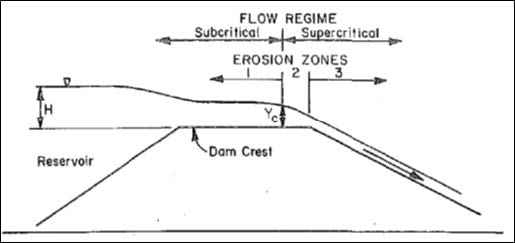
As equações da literatura aqui avaliadas para formação de brecha foram aquelas comumente citadas em trabalhos de estudo de ruptura hipotética de barragens de solo compactado e aquelas que possuem em sua proposta uma maior quantidade de casos históricos analisados.

 

Equações propostas por Froehlich (2008)

Informações a respeito de rupturas ocorridas no passado, bem como estudos experimentais, sugerem que a brecha se desenvolva, inicialmente, triangular, até atingir sua elevação mais baixa, quando começa a se expandir lateralmente até atingir um formato trapezoidal (FROEHLICH, 2008). A Figura 3 representa este desenvolvimento da brecha.

A fim de aplicar métodos empíricos para determinação da formação da brecha, Froehlich (2008) utilizou dados de 74 casos de ruptura de barragens, dos mais variados tipos de estruturas. Dentre estas estruturas estão barragens de solo homogêneo, barragens zonadas, barragens de solo e enrocamento e barragens com núcleo impermeável.

Figura 2 – Etapas de formação da brecha por galgamento. Fonte:Howard et al., 2009.

Figura 3 – Proposta de mecanismo para abertura da brecha. Fonte: FROEHLICH (2008).

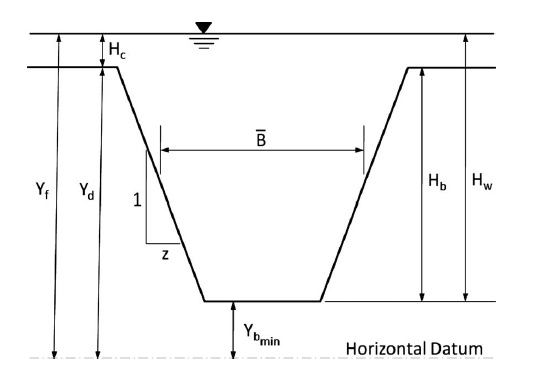
A Figura 4 exemplifica as dimensões de uma brecha trapezoidal (FROEHLICH, 2008). Nesta figura observa-se que ? ̅  ou ?_???é a largura média da brecha, ?_? a altura da brecha, z o fator de inclinação, ?_? a altura de água em relação ao fundo da brecha no momento da ruptura, ?_? a elevação do reservatório no qual se inicia a formação da brecha, ?_? é a profundidade crítica de overtopping e ?_???? indica a altura da barragem em que não se formou brecha.

Froehlich (2008) propôs a seguinte formulação para a estimativa da largura média da brecha (? ̅ ):

Equação 1

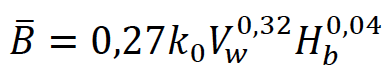
Na qual ?₀ é 1,3 ou 1,0 para rupturas por galgamento e outros modos de ruptura, respectivamente; ?_? é a altura da barragem (m) e ?_? é o volume de água contido no reservatório no momento da ruptura (m³).

Para o fator de inclinação (z) foram propostos valores iguais a 1,0 e 0,7 para rupturas por galgamento e outros modos de ruptura, respectivamente.

Ainda segundo Froehlich (2008), o tempo de formação da brecha proposto segue a Equação 2.

Equação 2

Figura 4 – Parâmetros geométricos de uma brecha trapezoidal. Fonte: FROEHLICH (2008).

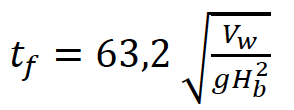
Equações propostas por Froehlich (2016)

Os equacionamentos desenvolvidos por Froehlich foram desenvolvidos com base em 63 casos de ruptura de barragens, em 1995. Posteriormente, em 2008, esse estudo foi revisado com base em 74 casos históricos de ruptura. Em 2016 o estudo foi atualizado, tendo como base 111 casos de ruptura de barragens. As equações atualizadas em 2016 são apresentadas a seguir para largura média da brecha:

Equação 3

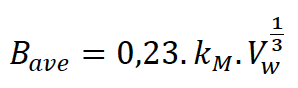
Na qual:

• B_ave: Largura média da brecha (m);
• k_M: coeficiente do modo de falha, sendo 1,0 para erosão interna e 1,5 para galgamento;
• V_w: volume de água acima da brecha no momento da falha (m³).

Para o fator de inclinação (z) foram propostos valores iguais a 1,0 e 0,6 para rupturas por galgamento e erosão interna, respectivamente. Para tempo de formação de brecha a seguinte equação foi proposta:

Equação 4

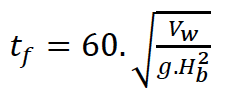
Na qual:

• V_w: volume de água acima da brecha no momento da falha (m³);
• H_b: altura da brecha (m);
• t_f: tempo de formação da brecha (h).

 

Equações propostas por Xu e Zhang (2009)

Os autores utilizaram 75 casos de ruptura de barragens dentre as quais estão barragens de solo homogêneo, barragens zonadas, barragens de enrocamento e barragens de face de concreto.

As equações propostas possuem coeficientes que levam em consideração não apenas o tipo de ruptura, mas também a erodibilidade da barragem. A erodibilidade da barragem leva em conta não apenas o tipo de material constituinte da barragem, mas também as condições de compactação do maciço, principalmente para aqueles formados por materiais finos, o ano de construção da estrutura e a geometria do maciço.

Briaud (2008 apud XU e ZHANG 2009) considera que materiais como enrocamento e areia possuem uma erodibilidade que varia de média a baixa, enquanto materiais argilosos e siltosos estão associados a valores de erodibilidade média a alta. Quanto à compactação do material, este mesmo autor aponta que a resistência a erosão cresce com a compactação do maciço para solos compostos principalmente por materiais finos.

As equações propostas por Xu e Zhang (2009) para a geometria da brecha são apresentadas a seguir. Estas formulações indicam a altura da brecha (Equação 3.3), a largura do topo da brecha e a largura média da brecha:

Equação 5

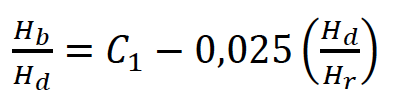
Em que ?_? é a altura da brecha (m), ?_? é a altura da barragem (m), ?_? é a variável de controle utilizada na regressão (15 m), ?₁=1,072; 0,986 e 0,858 para barragens de alta, média e baixa erodibilidade, respectivamente.

Equação 6

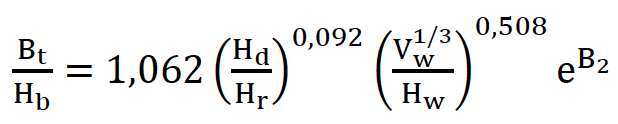
Em que ?₂= ?₃+?₄+?₅ sendo ?₃= 0,061; 0,088 e – 0,089 para barragens com núcleo argiloso, de face concretada e de seção homogênea/zoneada, respectivamente; ?₄= 0,299; -0,239 para overtopping e piping, respectivamente; ?₅ = 0,411; -0,062; -0,289 para erodibilidade da barragem alta, média e baixa, respectivamente.

Equação 7

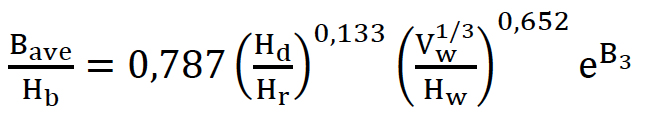
Na qual ?₃= ?₃+?₄+?₅ sendo ?₃= – 0,041; 0,026 e – 0,226 para barragens com núcleo argiloso, de face concretada e de seção homogênea/zoneada, respectivamente; ?₄= 0,149; -0,389 para overtopping e piping, respectivamente; ?₅ = 0,291; -0,14; -0,391 para erodibilidade da barragem alta, média e baixa, respectivamente.

Quanto ao tempo de formação da brecha, a seguinte equação foi proposta

Equação 8

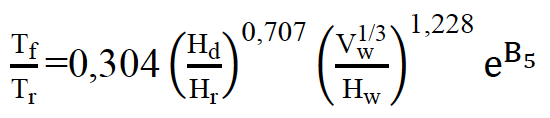
Na qual T_r é a variável de controle utilizada na regressão (1 h), ?₅= ?₃+?₄+?₅ em que ?₃= – 0,327; -0,674 e -0,189 para barragens com núcleo argiloso, de face concretada e de seção homogênea/zoneada, respectivamente; ?₄= -0,579; -0,611 para overtopping e piping, respectivamente; ?₅ = -1,205; -0,564; 0,579 para erodibilidade da barragem alta, média e baixa, respectivamente.

 

3. METODOLOGIA

Objetivando simular a ruptura de uma barragem por galgamento e a porcentagem de material escoado proveniente do reservatório, construíram-se diversos maciços em um canal no Centro de Pesquisas Hidráulicas da UFMG (CPH), levando em conta os diferentes aspectos a seguir apresentados.

Para a realização dos ensaios, e posterior interpretação dos resultados obtidos, foi necessário construir um modelo reduzido da barragem estudada. Para isso, primeiramente, determinou-se a escala geométrica do modelo, adotada igual a 1:100 para que fosse possível utilizar a infraestrutura disponível no CPH. Ressalta-se que foi adotado o modelo em escala reduzida com leito fixo, em que o leito sob a barragem não sofre processos erosivos, em razão das limitações de infraestrutura disponível para realização dos ensaios (canal em acrílico).

Para relacionar a geometria do modelo com a geometria da estrutura real, utilizou-se conceitos da teoria da semelhança hidráulica. Segundo esta teoria, para determinar a relação entre os valores observados no modelo e os valores reais, denominada escala, é necessário analisar conceitualmente o problema tratado e avaliar quais fenômenos hidráulicos prevalecem.

O processo de galgamento de uma barragem é essencialmente um escoamento livre em declividades fortes, que resulta em escoamentos em regime supercrítico e turbulento (POWELEDEGE, 1989b). Mesmo na hipótese de ocorrência de escoamento subcrítico em algum ponto do domínio simulado, é sabido que nestes casos os escoamentos livres ocorrem em regime turbulento. Desta forma, o aspecto a preservar na determinação das escalas é a similaridade do número de Froude (JULIEN,2002). Para melhor compreensão das transformações dos valores entre protótipo e modelo adotadas neste estudo, é necessário considerar que:

• A aceleração da gravidade no modelo e no protótipo é a mesma, assim ?? = ?? ?? = 1;
• O modelo usa água como fluido, e, uma vez que a escala para aceleração da gravidade é 1, as escalas para densidade (??), peso específico (??), viscosidade dinâmica (??) e viscosidade cinemática (??) são também unitárias.

Uma vez que foi construído um modelo isotrópico, as escalas vertical e horizontal serão as mesmas (Lr) e, assim, a escala de área e volume são respectivamente (JULIEN, 2002):

Equação 9

Equação 10

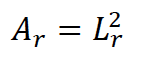
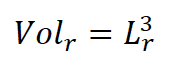
Mantendo-se a similaridade do número de Froude, sendo unitária a escala da aceleração da gravidade, tem-se que:

Equação 11

Equação 12

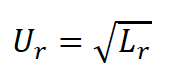
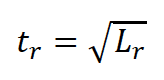
A escala para vazão será então definida por:

Equação 13

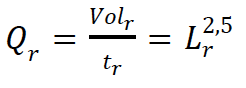
Para a realização dos ensaios optou-se por utilizar uma borracha de granulometria similar à areia para substituir o solo e o rejeito (Figura 5). Esta decisão levou em conta estudos já realizados no CPH, em que se constatou que os grãos de borracha de pneus moídos possuem densidade relativa variando entre 1,140 e 1,240 (CARVALHO et al., 2014), além deste material ser de fácil aquisição e gerar menos problemas técnicos aos equipamentos do laboratório.

A borracha utilizada teve sua curva granulométrica determinada pelo ensaio padrão da ABNT (NBR 7181/84). O material é classificado como areia grossa segundo esta norma da ABNT, ou areia siltosa conforme norma da ASTM.

Contudo, para que este material fosse utilizado na construção do maciço no modelo, seria necessário dar coesão ao mesmo. Optou-se por utilizar argamassa ACI como material coesivo, por se um material de fácil aquisição. Realizaram-se ensaios de cisalhamento direto para determinar qual a proporção entre argamassa e borracha levaria, em escala, a uma coesão esperada para barragens em escala real. Por fim, observou-se que os resultados obtidos através da correlação de coesão entre modelo reduzido e escala real não representavam a erodibilidade do material, e concluiu-se que no caso específico deste modelo representar a erodibilidade do material é mais importante que representar a coesão.

Assim, a coesão adotada no modelo de 0,62 Pa equivale, no protótipo, a uma coesão de 161,2 kPa. Este valor obtido é muito maior do que aqueles normalmente observados em maciços de solo compactado. Contudo, utilizar valores menores de coesão no modelo impossibilitaria a realização do experimento. Para todos os métodos esperou-se 24h a partir da construção para simulação da ruptura nas mesmas condições dos testes de cisalhamento direto. O maciço foi construído com as seguintes dimensões: 20m de altura; 40 cm de largura (base); 89 cm de extensão, sendo 40 cm no talude de montante, 6 cm na crista e 43 cm no talude de jusante, representando um arranjo de barragem com taludes montante e jusante 1V:2H, largura de crista igual a 6 m e berma no talude de jusante com 3m de largura.

Figura 5 – Grãos de borracha de pneus utilizado como material principal nos ensaios.

Para conformação do modelo reduzido final foram utilizadas ao todo 6 metodologias construtivas, as quais se diferem em razão de melhorias incrementais implementadas em razão de problemas identificados nas etapas anteriores. As metodologias são citadas a seguir e aquela que apresentou melhor resultado é detalhada: Maciço sem filtro e com crista em elevação única; Maciço sem filtro e com crista em elevação variável; Maciço com filtro; Maciço com lixas no fundo do canal; Maciço com lixas nas paredes laterais e no fundo do canal; Maciço com lixas nas paredes laterais e parcialmente no fundo do canal.

Dentre as metodologias aplicadas observou-se que, para construção do maciço, é necessário aumentar o atrito entre a borracha do maciço e os vidros do canal, evitando assim escorregamento da estrutura. Contudo, as lixas aplicadas não podem estar cobrindo totalmente o fundo do canal onde se construirá o maciço, pois estas podem atrapalhar a formação da brecha de ruptura.

Assim, a metodologia mais adequada foi a de maciço com lixas nas paredes laterais e parcialmente no fundo do canal, sendo esta a detalhada a seguir. Neste formato as lixas no fundo do canal, além de estarem posicionadas nos cantos, também foram inseridas fitas do fundo diagonalmente dispostas em espessuras menores (Figura 6 a). Ainda assim, verificou-se necessário deixar o centro livre como forma final (Figura 6 b). Além das fitas no fundo também foi necessário colar uma faixa em cada lateral (Figura 6 c)

Em todas as simulações realizadas, o volume de borracha depositado junto ao maciço, a fim de simular o rejeito presente no reservatório foi igual a 66 L, enquanto o volume de água contido no canal, sem causar o galgamento da barragem, era igual a 364 L, totalizando assim um volume de 430 L contidos no reservatório da barragem.

A relação de escala para volume apresentada anteriormente permite concluir que o volume armazenado no modelo corresponde, em escala real a 430.000 m³. Para um maciço de 20 m de altura considera-se o volume armazenado comparável ao de muitas estruturas reais, podendo a estrutura construída em escala reduzida ser comparada, em escala real, a um dique de contenção de sedimentos.

Uma vez que se deseja romper a estrutura por galgamento, foi necessário manter uma vazão fixa a fim de simular a cheia que levaria a barragem a galgar e, consequentemente, à sua ruptura. Os experimentos mostraram que vazões muito baixas não causavam a erosão desejada no maciço, que acabava rompendo por saturação e deslizamento de sua estrutura. Através das tentativas realizadas, concluiu-se que a vazão mais adequada para realização dos ensaios era de 8m³/h, o que corresponderia, em escala real, a uma vazão de projeto de 222 m³/s, novamente compatível a valores de vazões de cheias afluentes a reservatórios dessas estruturas com 10.000 anos de recorrência.

Figura 6 – Arranjo final das fitas antiderrapantes.

(a)

(b)

(c)

 

4. RESULTADOS

Após enchimento do reservatório, a vazão foi fixada em 8m³/h, vazão esta que se manteve constante até o final do ensaio. Conforme esperado, a erosão do talude de jusante se iniciou no pé da barragem e foi progredindo em direção a crista. A partir do momento em que o talude de jusante estava significativamente erodido, e a erosão estava quase na crista da barragem, (Figura 5.6) a erosão se tornou extremamente lenta, levanto aproximadamente 31 minutos entre a última erosão significativa no talude e a efetiva ruptura do maciço.

A Figura 7 apresenta a brecha obtida ao final do experimento. Destaca-se que no momento da ruptura a bomba foi desligada, assim, o volume que contribuiu para a formação da brecha foi apenas aquele contido no canal, 430 L. Observa-se que a brecha não se formou totalmente, assim, a fim de comparar a brecha formada com aquela sugerida pela literatura, não utilizou a altura total da barragem como altura máxima da brecha, mas sim a altura obtida no ensaio realizado.

A altura média obtida para a brecha neste ensaio foi de 10,5 cm, enquanto sua largura foi de 24,5 cm. O tempo de formação da brecha neste experimento foi de 0,67 min. Para a brecha obtida aplicaram-se as equações de Froehlich (2008), Froehlich (2016) e as equações propostas por Xu e Zhang (2009) para um maciço homogêneo e de erodibilidade média. A Tabela 1 a seguir apresenta os valores obtidos, em escala real, no experimento e pela aplicação das equações citadas.

Tabela 1-Valores obtidos para geometria e tempo de formação da brecha em maciço com lixas nas paredes laterais e parcialmente no fundo do canal

	Experimento	Froehlich (2008)	Froehlich (2016)	Xu e Zhang (2009) – Erodibilidade Média
Volume (m³)	430.000
Altura da Brecha (m)	10,5
Largura Média da Brecha (m)	24,5	24,5	26,0	22,6
Tempo de Formação da brecha (h)	0,11	0,35	0,33	0,70

Figura 7 – Brecha sendo formada durante experimento em maciço com lixas nas paredes laterais e parcialmente no fundo do canal (a) e configuração final após esvaziamento do reservatório (b)

(a)

(b)

 

5. CONCLUSÕES

Diversas dificuldades foram encontradas neste trabalho seja por limitações de recursos disponíveis para os modelos reduzidos ou pela limitação de tempo hábil para contornar os problemas identificados e aplicar as soluções propostas. Assim, a seguir serão listas as recomendações para futuros trabalhos nesta linha de pesquisa:

• Este tipo de modelo trabalhado (modelo de leito fixo) não permite a erosão da fundação, aumentando significativamente o tempo entre o início do galgamento e a efetiva ruptura da barragem. Assim, recomenda-se que seja pesquisado a importância da condição de fundação para a formação da brecha;
• É desejável que se a simulação ocorra em um canal mais largo do que o utilizado, a fim de tentar evitar influência do acrílico e incertezas em relação a esta condição de canal estreito;
• Observou-se que não é possível trabalhar com a coesão em escala e obter a erodibilidade desejada. Assim, recomenda-se que seja colocada em escala a erodibilidade, e não a coesão;
• Sugere-se que seja utilizado outro material para dar coesão a borracha, e não a argamassa. Este material coesivo trabalhado possui areia em sua composição e esta acaba se misturando na borracha.

Independente das incertezas no modelo reduzido aqui apresentadas entende-se que o cálculo da largura da brecha possui representatividade aceitável, enquanto o tempo de formação da brecha não apresentou neste estudo boa aderência.

Diversas são as incertezas em um estudo de ruptura hipotética, e estas vão além daquelas estudadas e discutidas neste trabalho. Com isso observa-se a necessidade de mais estudos nesta área, uma vez que parâmetros como formação da brecha de ruptura são informações fundamentais para a construção do hidrograma de ruptura, cuja propagação permitirá definir a envoltória de inundação na área a jusante da barragem, a qual tem como principal objetivo auxiliar no planejamento das ações de emergência e salvamento de vidas humanas.