Modelagem de fluxo hiperconcentrado na ruptura hipotética de pilha de resíduo industrial

INTRODUÇÃO

A disposição de rejeitos de mineração ainda é um grande problema no Brasil. De acordo com o Comitê Brasileiro de Barragens (CBDB, 2011), por muito tempo os resíduos gerados pelas atividades de mineração foram descartados diretamente sobre o solo ou em cursos d’água. Além disso, após as rupturas das barragens de Fundão, em Mariana (2015), e Córrego do Feijão, em Brumadinho (2019), foi intensificada a busca por metodologias alternativas de disposição de rejeitos, como os empilhamentos à seco, visando maior segurança nessa etapa do processo produtivo (ALVES, 2020).

Nesse sentido, as pilhas de rejeitos e pilhas de estéril são alternativas para minimizar os impactos associados à sua ruptura, seja em perdas de vidas humanas ou no meio ambiente. Essas estruturas se caracterizam por apresentar material não-saturado e ter sua deposição feita com maior controle tecnológico durante sua construção. Mesmo assim, como toda estrutura da engenharia, essas estruturas são dimensionadas para atenderem à fatores de segurança de estabilidade, envolvendo, então, incertezas e variabilidade das características do material, e consequentemente probabilidade de falhas.

Nas pilhas de rejeitos a concentração volumétrica de sólidos é alta, dado seu considerável grau de compactação, tornando o escoamento pós ruptura em um fluxo hiperconcentrado. Esse fluxo pode ser caracterizado como um escorregamento de uma superfície crítica de ruptura, que difere do método de ruptura e escoamento gerado a partir da ruptura de barragens, em que geralmente ocorre a abertura de brechas com escoamentos de lamas com menores concentrações volumétricas de sólidos. Isso significa que, para pilhas, não é possível adotar as mesmas premissas utilizadas em barragens de água e de rejeitos líquidos ou pastosos. Dessa forma, admite-se que este material escoaria com forte influência do contato entre suas partículas, com a ocorrência de escorregamentos de massa devido a instabilização de parte da estrutura e se propagaria como um fluxo hiperconcentrado.

Logo, o objetivo deste trabalho foi simular a propagação de um fluxo hiperconcentrado em uma ruptura hipotética de pilha de rejeitos. Esse trabalho auxiliará na parametrização e determinação de metodologias mais eficazes de avaliação para rupturas hipotéticas de pilhas de rejeitos.

 

CARACTERIZAÇÃO DA ESTRUTURA

A pilha em questão está localizada em um empreendimento de metalurgia dos metais não ferrosos que visa a obtenção de zinco metálico e suas ligas e óxido de zinco. Ela possui aproximadamente 30 m de altura e volume aproximado de 4,0 x 10⁶ m³.

 

DEFINIÇÃO DE METODOLOGIA

A metodologia baseou-se nos seguintes passos:

1. Identificação da seção mais crítica (maior altura, maior nível piezométrico, menor fator de segurança, etc…);

2. Utilização do software Slide2 para determinação da superfície de estrutura, pós ruptura;

3. Volume mobilizado determinado pela união do perfil obtido pelo Slide2 e a forma em planta da ruptura, conforme metodologia de Blight, 2010;

4. Propagação do rejeito no software RiverFlow2D considerando o modelo de Coulomb, adequado para materiais mais secos (maior concentração de sólidos).

 

1 – Seção crítica

Devido ao controle tecnológico utilizado na construção das pilhas (grau de compactação, controle do nível freático, condição não-saturada), o modo de falha associado a estas estruturas é a instabilização. Esse modo de falha está associado ao cálculo do fator de segurança (FS). Assim, quando a resistência ao cisalhamento é menor que a tensão de cisalhamento, ou seja, FS < 1, o material empilhado se encontra em uma situação de instabilidade e pode ocorrer movimentos de massa, nesse caso, escorregamentos.

Foi utilizado o software Slide2 da Rocscience para verificação do FS e determinação da superfície de ruptura. Para a simulação, foi considerado o método de Equilíbrio-Limite, cunha circular, método de Spencer, e parâmetros drenados como dados de entrada no modelo.

A análise de estabilidade obtida no Slide2 demonstra o menor fator de segurança da pilha em questão é de 1,366 em sua seção de maior altura. É possível destacar que, apesar do FS maior que 1, o resultado do Slide indica que a superfície mais frágil é e representada por aquela com menor FS.

 

2 – Superfície de ruptura

Determinada a seção mais crítica, foi utilizado o resultado obtido na análise anterior para definição da geometria da superfície de ruptura em planta.

De forma a obter um cenário mais crítico, adotou-se a hipótese de que após o primeiro escorregamento, a superfície de ruptura tenderia a aumentar, devido ao desconfinamento inicial de parte do solo. Assim, foram realizadas simulações consecutivas no software Slide2, supondo este desconfinamento, até a obtenção de uma geometria estável.

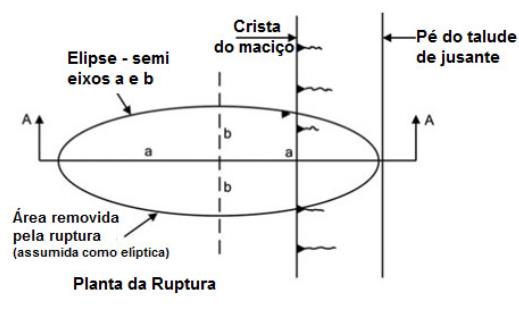
Para determinação da geometria em planta da superfície de ruptura, foi utilizado a hipótese de que essa geometria pode ser aproximada a uma elipse, conforme mostrado no trabalho de Blight (2010). Se observar em planta, a superfície de ruptura na barragem se assemelha a uma elipse (BLIGHT, 2010), inclusive em pilhas, como é possível observar na Figura 2.

A proposição de Blight (2010) pode ser sustentada pela observação das geometrias de dezenas de rupturas descritas em casos históricos. A definição das dimensões dessa elipse e a associação com as características geotécnicas do rejeito são apresentados no trabalho de Ribeiro et al. (2016).

Figura 2 – (a) Estimativa do volume de ruptura através da aproximação à elipse (Fonte: Ribeiro et al., 2016). (b) exemplo de ruptura de pilha com formato elipsoidal

(a)

(b)

Dessa forma, com o conhecimento do valor do eixo a da elipse, extraído pela análise do Slide2, é possível encontrar o eixo b utilizando a equação proposta por Ribeiro et al. (2016). Os autores relacionaram os eixos a e b de casos históricos de rupturas de barragens com geometria na forma de elipse. Assim, obtiveram a relação em planta entre comprimento (eixo a) e a largura da ruptura (eixo b).

Equação 1

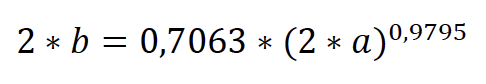
Após definição da geometria, foi construído no software QGis 3.16 o raster referente a essa superfície de ruptura (Figura 3) e calculado o volume mobilizado.

Figura 3 – Vista em planta e perfil transversal da forma mobilizada.

 

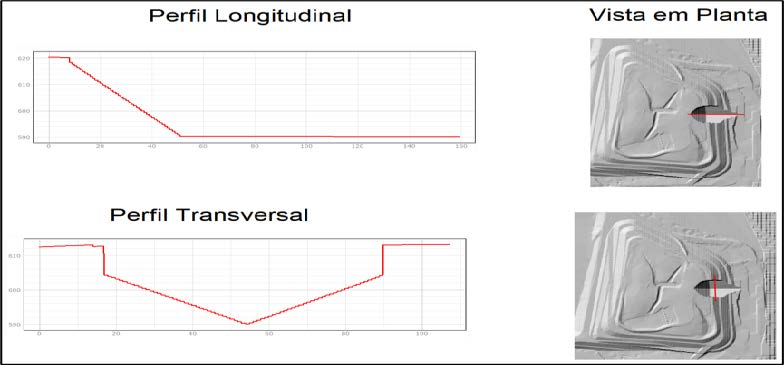
3 – Volume mobilizado

Diferentemente das barragens de rejeito em polpa, que chegam a mobilizar 100% do material, as pilhas dificilmente mobilizam todo o material empilhado, limitando-se à mobilização de uma fração de seu volume total, como ocorrido em diversos casos reais.

A definição do volume mobilizado se deu a partir do estudo de determinação da superfície de ruptura explicitado no item anterior. Assim, com base na metodologia adaptada de Blight (2010), o volume mobilizado será formado pela forma da elipse (em planta) e da superfície (em perfil).

 

4 – Propagação do escoamento

Após a definição do volume mobilizado, utilizou-se o modelo matemático-computacional denominado RiverFlow2D, desenvolvido pela Hydronia LLC, em sua versão 07.50, para a propagação de cheias de ruptura e consequente definição de áreas potencialmente atingidas. O modelo combina volumes finitos de transporte hidrológico e hidrodinâmico de leito móvel e poluentes para rios, estuários, áreas costeiras e planícies de inundação. Para simular a propagação da onda de ruptura, o modelo utiliza uma grade não estruturada com células triangulares, permitindo que o campo de fluxo seja bem definido. Para o presente trabalho, foram adotadas células de comprimento característico de até 5 m. O passo de tempo computacional (Δt) é variável pelo software de forma a obter estabilidade no modelo.

Para funcionamento do modelo, é preciso a entrada de alguns dados básicos, como as condições de contorno. A condição de contorno de entrada do modelo foi a geometria atual da pilha e a geometria final, após o escorregamento. Não foi necessária a inserção de uma condição de contorno de saída, dada a reduzida extensão da mancha dos cenários avaliados.

No modelo, foi considerada a equação de resistência ao fluxo denominada Granular Material, utilizada em análises de fluxos de detritos (e. g.: CROSTA, CUCCHIARO e FRATTINI, 2003). Essa equação sugere sua utilização, haja vista que a medida que a concentração volumétrica do material aumenta, a probabilidade de contato entre partículas também aumenta. Em concentrações grandes o suficiente, esse contato se torna permanente, quando as partículas deixam de estar suspensas em um fluido e passam a escorregar umas em cima das outras. Com interação predominante entre as partículas passando de colisão para fricção, o equacionamento que caracteriza seu movimento deve considerar também processos geotécnicos. Dessa forma, utiliza-se o modelo de Morh-Coulomb para simular a mobilização do material, já que o processo passa a ter semelhanças com um escorregamento de massa (FLOYD et al., 2020). Para uso desta equação, os parâmetros de entrada para essa simulação foram: densidade de sólidos de 2,79 g/cm³ (conforme ensaios feitos com o material da pilha), ângulo de atrito residual do material escorregado e a concentração volumétrica do material mobilizado.

De forma conservadora, foi considerado que o material presente no interior da superfície de ruptura estará sujeito a resistência não drenada residual. Isto se justifica pela velocidade em que acontece o escorregamento, considerado um movimento rápido, e na condição de desconfinamento do material escorregado, não tendo mais as características geotécnicas do momento anterior ao escorregamento. Assim, foram definidos os seguintes cenários:

• Cenário de ruptura extremo: foi utilizado o valor de referência de 0,05, correspondente a razão de resistência não drenada liquefeita (?_? /?′_1?) proposta por Olson (2001), que é o valor mínimo possível de aplicação (sendo a condição mais crítica), e resulta em um ângulo de atrito (?_?) de 2,8° (conforme Equação 2). O valor de ?_? é apenas no material presente no interior da superfície de ruptura.
• Cenário de ruptura provável: foi considerado que o material do interior da superfície de ruptura estará condicionado a resistências não-drenadas de pico, o qual é um valor maior do que a resistência não drenada liquefeita, de acordo com Olson (2001). Assim, foi utilizado o valor de referência de 0,2, correspondente a razão de resistência não drenada de pico, e resultou em um ângulo de atrito (?_?) de 11,30° (conforme Equação 2). Novamente, o valor de ?_? é apenas referente ao material presente no interior da superfície de ruptura.

Equação 2

 

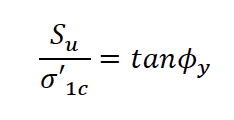
RESULTADOS E DISCUSSÃO

Determinação da superfície de ruptura e volume mobilizado

Após simulação no Slide 2, foi obtido a seção e a superfície crítica de ruptura. Para isso, foram realizadas 4 simulações consecutivas até que fosse obtida uma superfície final estável, ou seja, como fator de segurança superior a um. Na Figura 4 é mostrada essa superfície de ruptura e a dimensão do eixo a da elipse em planta, que resultou em um valor de aproximadamente 115 metros (referente ao valor de 2 vezes a dimensão a), como mostrado na Figura .

Na sequência foram obtidos os valores de volumes relativos ao rejeito da pilha (Tabela 1). é possível destacar que a porcentagem do volume de rejeito mobilizado foi baixa, 1,74%, quando relacionado com o volume total de rejeitos na pilha (3,8.10⁶ m³).

Tabela 1 – Volume mobilizado para os cenários extremo e provável

Descrição	Obtenção	Volumes cenários extremo e provável (m³)
Volume atual de rejeitos no reservatório	Curva Cota-Volume	3.834.379
Volume total mobilizado	QGIS	73.943
Volume rejeito mobilizado	QGIS	66.865
Volume maciço mobilizado	QGIS	7.078
Volume de sólidos maciço	90% volume maciço QGIS	6.370
Volume de água no maciço (m³)	Vol. Maciço mobilizados QGIS – Vol. Sólidos Maciço	708
% vol rejeito mobilizado	–	1,74%

 

Propagação do escorregamento no cenário de ruptura provável

No cenário de ruptura provável, a mancha percorreu 50 m até chegar à extensão máxima de propagação, quando sua velocidade de escoamento chega a zero. Foram inseridas seis seções representativas, ST-01 a ST-06, a primeira imediatamente a jusante da superfície de ruptura e as seguintes ao longo do trecho afetado. Devido à pequena extensão da mancha nesse cenário, apenas a primeira, ST-01, foi atingida, como ilustrado na Figura 5.

Figura 5 – Representação ilustrativa da pilha no tempo inicial e no tempo final da ruptura – Cenário Provável.

Na Figura 6 é apresentado o hidrograma da seção ST-01, única localizada no talvegue a jusante da pilha atingida pela mancha do cenário provável. A vazão de pico na seção foi de 6,11 m³/s.

Figura 6 – Propagação da Onda de Ruptura Extrema – ST-01.

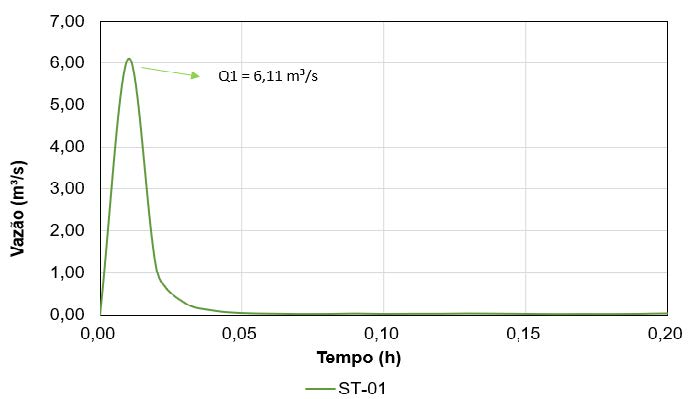
Apesar da baixa extensão da mancha, a onda de ruptura chega rapidamente, em menos de 1 minuto, até a seção ST-01. A onda apresenta uma profundidade, na seção, de 2,05 m e uma velocidade máxima de 0,50 m/s.

 

Propagação do escorregamento no cenário de ruptura extremo

No cenário de ruptura extremo, a mancha percorreu 550 m até chegar à extensão máxima de propagação, quando sua velocidade de escoamento chega a zero. Na Figura 7 é apresentado os hidrogramas das seções localizadas no talvegue da pilha de rejeitos avaliada. A vazão de pico foi de 306 m³/s, sofrendo grande abatimento nas seções seguintes.

Figura 7 – Propagação da Onda de Ruptura Extrema – ST-01 e ST-02.

 

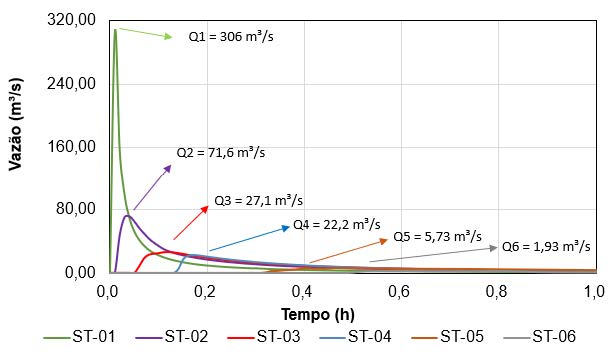
Comparação das manchas de propagação

A área potencialmente afetada por danos diretos, ou seja, por processo de escorregamento, em caso de ruptura da pilha, tanto para o cenário provável, quanto para o cenário extremo, está localizada próxima a pilha. Para o cenário extremo, a mancha percorreu cerca de 550 m no talvegue a jusante da pilha. Já o cenário provável, apresentou uma mancha com 35 metros de comprimento. A largura inundada máxima foi de, aproximadamente, 215 m no cenário extremo e 122 m no cenário provável. As duas manchas são mostradas na Figura 8.

Figura 8 – Manchas de inundação dos cenários extremo e provável.

 

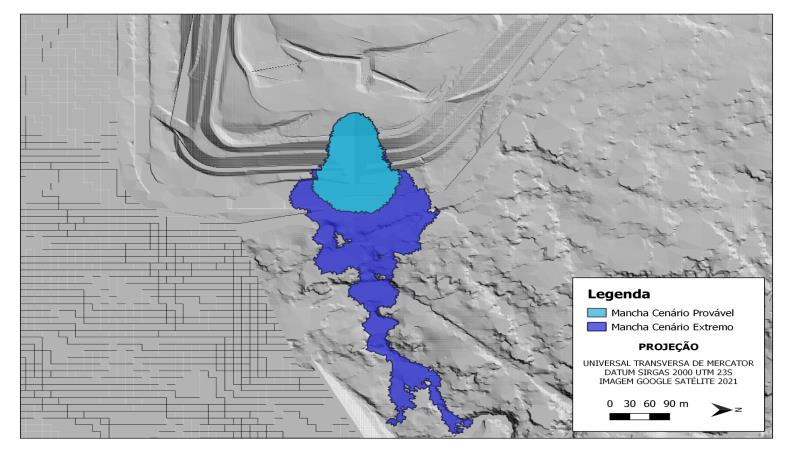
CONCLUSÕES

A modelagem de fluxo hiperconcentrado realizado neste estudo de ruptura hipotética determinou o contorno de propagação da onda de ruptura, com a delimitação das áreas potencialmente inundáveis a jusante, de acordo com as premissas, critérios e metodologias descritas no presente documento.

No presente estudo foram definidos dois cenários de simulação: ambos cenários de ruptura, considerando a geometria atual da pilha de rejeitos (El. 622,0 m) e equação de resistência ao fluxo Granular Material. Um cenário mais provável, que considerou a ruptura em uma condição menos conservadora (ângulo de atrito de 11,3º), e outro extremo, considerando a redução da resistência do material mobilizado (ângulo de atrito de 2,8º).

Os resultados indicam que a metologia aplicada pode ser adequada para simulação de fluxo hiperconcentrado em rupturas hipotéticas de pilhas. Devido a lacuna de conhecimento nesta área, sugere-se maiores investigações nesse tipo de ruptura e na propagação de escoamentos hiperconcentrados para que as previsões sejam mais próximas da realidade e os erros associados diminuídos.