Vítor Lages do Vale 1; Victoria Sofia Guimarães Braga 2; Clara Demattos Nogueira 3, Mariana Almeida Henriques 4; Malena Lúcia Sousa Freire de Melo 5
Rompimentos de barragens de rejeito geram fluxos hiperconcentrados, que são fenômenos instáveis no qual as propriedades do fluido são, geralmente, não-newtonianas. Para melhor caracterização dos fenômenos, foram coletadas e testadas amostras de sedimento, rejeito e resíduo de mineração. Foram comparados parâmetros como material de origem, densidade, granulometria, tensão de cisalhamento e viscosidade dinâmica, a fim de verificar correlações. Foram também estudados os coeficientes alfa e beta das equações de tensão de cisalhamento e viscosidade dinâmica em função da fração volumétrica, e os valores encontrados para as amostras estudadas estão dentro da faixa encontrada para os valores da literatura. Foi possível observar indícios de correlação positiva da densidade dos sólidos com os parâmetros α1 e β2, para ouro, e com α1, para o zinco. As regressões lineares múltiplas indicaram influência da granulometria, onde o aumento do diâmetro levou a redução dos parâmetros α1 e β2, para ouro, e β1, para zinco. Deve-se aumentar o número de amostras e características analisadas para introduzir mais robustez ao estudo.
Disruption of tailings dams generates hyper-concentrated flows that are unstable phenomena in which the fluid’s properties are generally non-newtonian. For better characterization of the phenomena, sediment, tailings and mining waste samples were collected and tested. Then, parameters such as type of material processed, density, granulometry, shear yield stress and viscosity were compared to verify correlations. It was also studied the alpha and beta coefficients of the shear yield stress and viscosity equations as a function of the volumetric fraction, and the values found for the studied samples are within the range found for the literature values. It was possible to observe evidence of a positive correlation of solids density with parameters α1 and β2 for gold, and with α1 for zinc. The multiple linear regressions indicated the influence of granulometry, where the increase in diameter led to the reduction of parameters α1 and β2 for gold and β1 for zinc. The number of samples and characteristics analyzed should be increased to introduce more robustness to the study.
INTRODUÇÃO
Rompimentos de barragens de rejeitos geram escoamentos hiperconcentrados, que são fenômenos instáveis e cujas propriedades dos fluidos são normalmente não-newtonianas, em razão da elevada concentração de sólidos. A ciência que caracteriza este tipo de escoamento é a reologia, campo científico que estuda o escoamento da matéria com suas mudanças de forma e fluxo, e os parâmetros como a viscosidade dinâmica, plasticidade, elasticidade e a fricção desses fluidos, mais especificamente, fluidos não-newtonianos.
Para compreender e modelar estes fenômenos com maior precisão, é necessário conhecer as caraterísticas destes sólidos a fim de utilizar os parâmetros e equacionamentos mais adequados. Os principais parâmetros que se busca conhecer ao modelar um fluxo não-newtoniano, conforme modelo de Bingham (1922), são tensão de cisalhamento e viscosidade dinâmica.
Para definir esses parâmetros que caracterizam o escoamento são necessário ensaios reológicos. Nesse sentido, alguns trabalhos buscaram avaliar associações e influências entre as propriedades físicas e reológicas dos rejeitos. Wang et al. (2018) analisaram o impacto do tipo de minério, diâmetro dos sólidos (D25, D50 e D75), concentração volumétrica e taxa de cisalhamento nas propriedades reológicas de rejeitos de ouro, cobre e ferro. Os autores observaram o impacto da composição e teor mineral, onde a tensão de cisalhamento e a viscosidade dinâmica foram maiores para rejeitos de minério de ferro e menores para rejeitos de ouro (WANG et al., 2018). Wang et al. (2018) verificaram ainda que para uma mesma concentração de sólidos, quanto maior o tamanho da partícula, menores são os valores de viscosidade dinâmica e tensão de cisalhamento.
Desriviers et al. (2019) investigaram os efeitos da composição mineralógica e da distribuição do tamanho da partícula na reologia de rejeitos de ouro e cobre. Esses autores também obtiveram que amostras com partículas mais grossas causam a diminuição da tensão de cisalhamento, e à medida que há acréscimo de fração fina, a tensão de cisalhamento aumenta (DESRIVIERS et al., 2019). A relação entre as características físicas e parâmetros reológicos pode permitir ainda o desenvolvimento de modelos preditivos, como realizado por Zengeni (2016). Com o uso de regressão, Zengeni (2016) obteve curvas reológicas de tensão de cisalhamento e viscosidade dinâmica de Bingham a partir das propriedades de densidade de sólidos, distribuição do tamanho e forma das partículas e concentração de sólidos, para aplicação no bombeamento de rejeitos de ouro.
Neste trabalho, foram avaliadas possíveis correlações entre parâmetros reológicos e características físicas de 22 amostras coletadas em barragens de rejeito de mineração e indústria e sedimentos, tendo sido avaliadas a densidade específica e a distribuição granulométrica. Com isso, busca-se apresentar uma análise de validação de dados obtidos, sem substituir os ensaios reológicos.
Os valores para os coeficientes da regressão linear das curvas de tensão de cisalhamento por concentração volumétrica e viscosidade dinâmica por concentração volumétrica também são comparados aos encontrados na literatura, tendo como referência O’Brien e Julien (1988) e outros.
MATERIAIS E MÉTODOS
Caracterização física dos materiais
Para realização dos estudos, foram analisadas 22 amostras, sendo os dados obtidos de estudos desenvolvidos pela empresa HIDROBR Consultoria LTDA. As amostras foram coletadas majoritariamente no estado de Minas Gerais, sendo uma amostra no estado de São Paulo.
As características físicas analisadas foram densidade dos sólidos (ρs) (g/cm³), obtidas diretamente dos ensaios, e distribuição granulométrica. Pela curva granulométrica, foi possível definir os valores de D80 (μm), D60 (μm), D50 (μm), D30 (μm) e D10 (μm), além dos percentuais de areia, silte e argila, resultando na classificação dos solos conforme metodologia USDA.
Caracterização reológica dos materiais
Os ensaios reológicos das amostras foram realizados em laboratório com reômetros, permitindo a geração das curvas de tensão de cisalhamento e viscosidade dinâmica em relação à concentração volumétrica de sólidos (CV), interpretadas utilizando o modelo de Bingham (1922).
Conforme O’Brien e Julien (1988), a viscosidade dinâmica e a tensão de cisalhamento podem ser obtidas conhecendo-se os coeficientes de calibração para determinado rejeito e pela fração volumétrica, segundo as Equações 1 e 2, na qual ?? é a tensão de cisalhamento e ? é a viscosidade dinâmica do material.
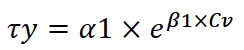
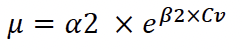
Assim, a partir dos valores encontrados para concentração volumétrica, tensão de cisalhamento e viscosidade dinâmica das amostras deste trabalho, realizou-se a regressão linear para as Equações 1 e 2, obtendo-se valores de α1, α2, β1 e β2 para cada amostra.
Aderência aos dados de literatura
De posse dos valores de α1, α2, β1 e β2 das equações que descrevem o comportamento reológico das amostras, realizou-se uma comparação dos valores médios e desvio padrão com os parâmetros obtidos por O’Brien e Julien (1988). Esses autores recolheram amostras de depósitos naturais de lama no Colorado Rock Moutains perto das cidades de Aspen e Glenwood Springs, além de outras literaturas, a saber Lida (1938), Dai et al (1980), Kang e Zhang (1980), Qian et al (1980), Chien e Ma (1958) e Fei (1981).
Correlação e regressão
Para entender o efeito das características físicas no comportamento reológico dos materiais, inicialmente buscou-se estabelecer correlações lineares entre as características físicas e os coeficientes que descrevem o comportamento reológico. Para isso, foi utilizado o coeficiente de correlação linear de Pearson, que é adimensional e varia de -1 a 1, onde o valor indica 1 correlação linear positiva perfeita, -1, negativa e 0 indica que não há correlação. Foi também utilizado o coeficiente de determinação R quadrado, que indica a “proporção da variância total da variável dependente Y que é explicada pelo modelo de regressão” (NAGHETTINI e PINTO, 2007, pg. 366).
Em seguida, considerando a complexidade do comportamento reológico e a dificuldade de ser explicado por um único parâmetro (ADIGUZEL e BASCETIN, 2019), buscou-se introduzir mais complexidade ao modelo, ao trabalhar com regressão linear múltipla. Esse modelo de regressão avalia o comportamento de uma variável dependente Y em função de múltiplas variáveis independentes Xi, e pode ser adotado se Y variar linearmente com as variáveis Xi (NAGHETTINI e PINTO, 2007).
Para analisar a existência de uma relação significativa entre a variável dependente e as variáveis independentes pode ser utilizado o “teste do F total” (NAGHETTINI e PINTO, 2007), sendo consideradas análises que tiveram intervalo de significância de 95% (F total < 0,05).
Para explicar os valores de α1, α2, β1 e β2 (variáveis dependentes), separadamente, foram considerados a densidade dos sólidos (g/cm³) e os diâmetros (variáveis independentes). Partindo da premissa da influência da origem do material em seu comportamento reológico, a regressão foi feita para as amostras de zinco e ouro, por serem os materiais com mais amostras. Dado o limitado número de amostras do mesmo material, foram analisadas apenas duas variáveis por vez.
RESULTADOS E DISCUSSÃO
Caracterização física dos materiais
Na Tabela 1 são apresentadas as 22 amostras utilizadas no presente estudo, com seus respectivos materiais de origem e densidades do sólido. Para identificá-las, a primeira letra se refere ao material de origem, o primeiro número é referente à barragem de onde a amostra foi retirada, e o segundo, ao número da amostra. Destaca-se que as amostras Z1 a Z3 são provenientes de resíduo de zinco, enquanto as amostras Z4 a Z6 são provenientes de rejeito de zinco.
| Identificação | Material de Origem | ρs (g/cm³) |
| B1 | Bauxita | 2,89 |
| B2 | 2,74 | |
| B3 | 2,85 | |
| S1.1 | Sedimento | 3,07 |
| S1.2 | 3,49 | |
| S1.3 | 3,03 | |
| S2 | 3,56 | |
| O1 | Ouro | 2,92 |
| O2.1 | 3,98 | |
| O2.2 | 3,90 | |
| O2.3 | 3,56 | |
| O3 | 2,88 | |
| O4 | 2,83 | |
| O5.1 | 2,88 | |
| O5.2 | 2,89 | |
| O5.3 | 2,88 | |
| Z1 | Zinco | 2,79 |
| Z2 | 3,19 | |
| Z3 | 3,11 | |
| Z4 | 2,91 | |
| Z5 | 2,93 | |
| Z6 | 3,08 |
A análise granulométrica das amostras é apresentada na Tabela 2, em que é possível observar que o diâmetro de referência D60 das amostras se ordena conforme o material de origem.
| Identificação | Material de Origem | D80 (μm) |
D50 (μm) |
D30 (μm) |
D10 (μm) |
D60 (μm) |
Média D60 (μm) |
Classificação USDA |
| B1 | Bauxita | 41,9 | 6,46 | 2,95 | 1,17 | 10,4 | 202 | Franco Siltosa |
| B2 | 786 | 330 | 186 | 59,0 | 443 | Areia | ||
| B3 | 295 | 97,9 | 25,0 | 2,08 | 151 | Franco Arenoso | ||
| Z1 | Zinco | 31,0 | 11,1 | 5,9 | 2,17 | 15,3 | 22,0 | Silte |
| Z2 | 28,0 | 7,10 | 3,47 | 1,29 | 9,60 | Franco Siltosa | ||
| Z3 | 8,73 | 3,78 | 2,00 | 0,89 | 4,66 | Franco Argilo Siltosa | ||
| Z4 | 131 | 65,0 | 19,1 | 2,84 | 87,6 | Franco Arenoso | ||
| Z5 | 29,4 | 8,59 | 4,18 | 0,408 | 12,2 | Franco Siltoso | ||
| Z6 | 6,75 | 0,992 | 0,205 | 0,001 | 2,56 | Franco Argilo Siltoso | ||
| S1.1 | Sedimento | 7278 | 248 | 82,3 | <1 | 574 | 282 | Franco Arenoso |
| S1.2 | 1341 | 160 | 106 | 42,9 | 220 | Areia | ||
| S1.3 | 265 | 93,7 | 30,0 | <1 | 122 | Franco Arenoso | ||
| S2 | 4796 | 105 | 39,4 | 2,98 | 212 | Franco Arenosa | ||
| O1 | Ouro | 92,7 | 47,3 | 23,4 | 4,21 | 55,9 | 53,7 | Franco siltosa |
| O2.1 | 66,6 | 60,3 | 28,6 | 5,21 | 63,5 | Franco | ||
| O2.2 | 56,9 | 20,4 | 8,49 | 2,85 | 29,8 | Franco Siltosa | ||
| O2.3 | 22,9 | 7,87 | 4,51 | 2,05 | 9,93 | Silte | ||
| O3 | 63,7 | 26,5 | 13,6 | 2,10 | 34,7 | Franco Siltosa | ||
| O4 | 104 | 46,9 | 20,1 | 3,96 | 61,7 | Franco Siltosa | ||
| O5.1 | 133 | 60,9 | 23,8 | 4,93 | 81,6 | Franco Siltosa | ||
| O5.2 | 121 | 49,6 | 16,7 | 4,06 | 70,0 | Franco Siltosa |
As amostras de sedimento apresentam maior média de diâmetro característico, uma vez que foram obtidas de diques de contenção de sedimentos. As demais amostras se classificam entre siltosas e arenosas, sendo aquelas amostras de material com origem na bauxita possuem duas das três amostras com maior percentual de areia (> 60%) e apenas uma classificada como siltosa (B1). As amostras com origem no zinco são todas siltosas, exceto Z4. Já as amostras de ouro se classificam principalmente como franco siltosa.
Caracterização reológica dos materiais
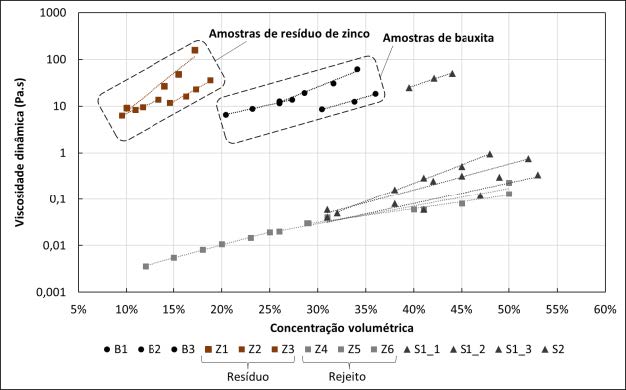
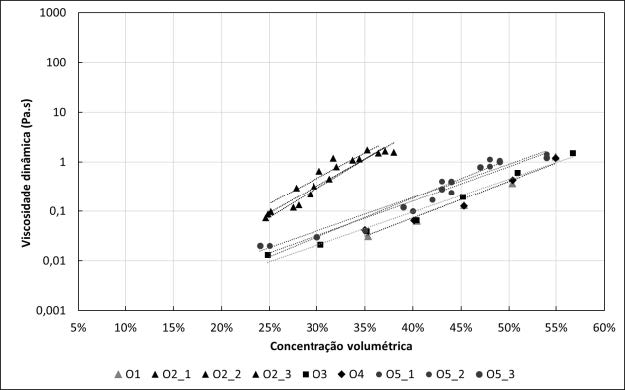
As curvas de tensão de cisalhamento e viscosidade dinâmica em relação à concentração volumétrica de sólidos (CV) são apresentadas nas Figura 1 a Figura 2, a partir das quais observa-se que as amostras estão agrupadas de acordo com os materiais de origem. Na Tabela 3 e Tabela 4 são apresentados os parâmetros α e β das curvas reológicas, definidas a partir de ajuste exponencial aplicados aos resultados das amostras.
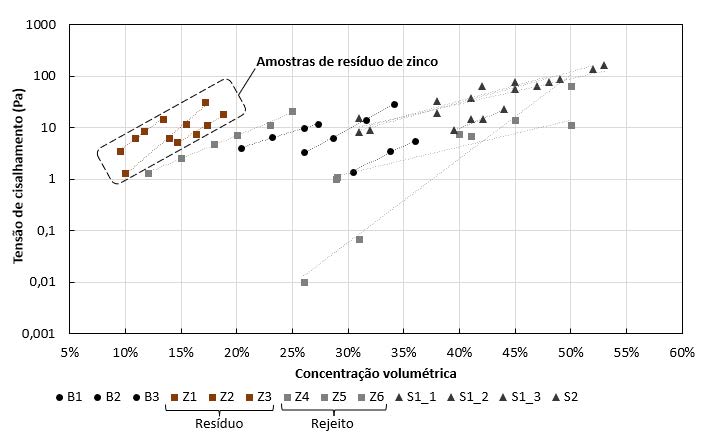 (a) (a) |
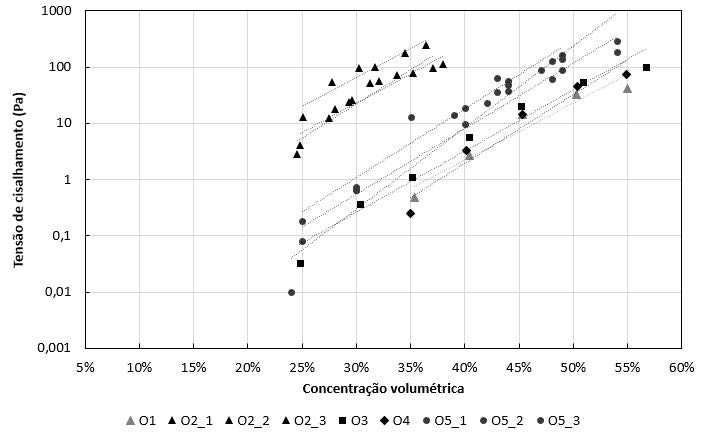 (b) (b) |
| Amostra | B1 | B2 | B3 | O1 | O2.1 | O2.2 | O2.3 | O3 | O4 | O5.1 | O5.2 | O5.3 |
| α1 | 3,0E-03 | 8,8E-04 | 1,7E-01 | 1,9E-04 | 5,0E-02 | 5,2E-03 | 1,7E-02 | 1,4E-04 | 2,5E-05 | 1,8E-04 | 2,4E-04 | 1,3E-05 |
| β1 | 26,85 | 24,35 | 15,63 | 23,39 | 23,92 | 27,89 | 23,99 | 25,07 | 28,13 | 26,83 | 28,07 | 33,38 |
| Amostra | Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | S1.1 | S1.2 | S1.3 | S2 | ||
| α1 | 1,6E-02 | 1,1E-01 | 6,1E-02 | 3,6E-02 | 7,6E-07 | 1,2E-01 | 1,3E-01 | 3,1E-01 | 1,2E-01 | 2,6E-03 | ||
| β1 | 43,07 | 37,04 | 30,16 | 11,90 | 37,52 | 20,02 | 13,76 | 11,31 | 13,77 | 20,61 | ||
 (a) (a) |
 (b) (b) |
| Amostra | B1 | B2 | B3 | O1 | O2.1 | O2.2 | O2.3 | O3 | O4 | O5.1 | O5.2 | O5.3 |
| α2 | 8,5E-02 | 1,3E-01 | 7,7E-01 | 3,4E-05 | 4,0E-04 | 8,4E-05 | 1,8E-04 | 2,0E-04 | 7,8E-05 | 2,6E-04 | 1,3E-04 | 3,7E-04 |
| β2 | 19,03 | 13,65 | 10,53 | 18,75 | 23,58 | 27,19 | 25,10 | 15,41 | 17,12 | 16,09 | 18,16 | 15,57 |
| Amostra | Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | S1.1 | S1.2 | S1.3 | S2 | ||
| α2 | 1,9E-01 | 9,9E-01 | 2,3E-01 | 4,1E-03 | 2,1E-03 | 7,9E-04 | 1,6E-04 | 1,3E-03 | 9,4E-04 | 4,7E-02 | ||
| β2 | 37,39 | 19,61 | 26,55 | 6,79 | 8,76 | 12,84 | 18,17 | 10,34 | 12,84 | 15,89 | ||
Na Figura 1 é possível ver um comportamento distinto para as amostras provenientes de resíduo de zinco, que apresentam elevados valores de tensão de cisalhamento para concentrações volumétricas (CV) mais baixas (de 10% a 20%), o que demonstra mais resistência ao escoamento por parte dessas amostras. As amostras de sedimento e rejeito de zinco foram ensaiadas para maiores valores de CV e possuem comportamento semelhante, exceto pela amostra Z6, que apresenta valores menores de concentração volumétrica em relação às demais amostras de rejeito de zinco. Na Figura 2 é possível constatar que as amostras de resíduo de zinco possuem valores de α2 e β2 elevados, indicando alta viscosidade dinâmica.
Em função do maior número de amostras de ouro, essas foram analisadas separadamente. Observa-se que as amostras da barragem 2 diferem-se das demais (Figura 1), ao apresentar maiores valores de α1, resultando em maiores valores de tensão de cisalhamento para a mesma concentração volumétrica. Além disso, observa-se que essas amostras foram ensaiadas para valores inferiores de CV, também indicando a dificuldade em escoar. Por outro lado, observa-se que os valores de β1 são semelhantes, representados pela inclinação das retas. Na Figura 2, as amostras da barragem 2 apresentam maiores valores de β2, indicados pela maior inclinação da reta. Novamente, os resultados em limites menores de CV indicam maior dificuldade de escoar.
Aderência aos dados de literatura
Para auxiliar na comparação dos valores das Tabela 3 e Tabela 4, foi elaborada a Tabela 5 em que é apresentada a análise estatística dos coeficientes encontrados. Pode-se observar que a média dos valores de α1 das amostras é cerca de 7 vezes menor que a média dos valores obtidos por O’Brien e Julien (1988) e 17 vezes menor, em relação às outras literaturas. Porém o desvio padrão observado é menor, o que indica menor variação dos valores. Apesar dos valores médios de β1 e β2 serem, respectivamente, maior e menor que os valores médios de O’Brien e Julien (1988) e outras referências, ainda sim são valores próximos. A média dos valores de α2 encontra-se acima das médias dessas referências. Salienta-se ainda que o valor médio das amostras deste estudo se encontra dentro da faixa do desvio padrão das amostras de O’Brien e Julien (1988) e das demais literatura analisadas.
| Parâmetro | α1 | β1 | α2 | β2 |
| Média Amostras | 0,053 | 24,848 | 0,112 | 17,698 |
| Média O’Brien e Julien (1988) | 0,355 | 20,610 | 0,088 | 21,940 |
| Média Outras Literaturas | 0,904 | 18,688 | 0,016 | 19,760 |
| Desvio Padrão Amostra | 0,080 | 8,473 | 0,259 | 7,025 |
| Desvio Padrão O’Brien e Julien (1988) | 0,836 | 6,257 | 0,201 | 8,973 |
| Desvio Padrão Outras Literaturas | 1,199 | 7,051 | 0,022 | 14,899 |
Verifica-se ainda que os valores de desvio padrão de todas as amostras são elevados em relação às médias dos valores observados, evidenciando a grande discrepância dos parâmetros entre as amostras avaliadas por cada um dos autores.
Correlação e regressão
Na Tabela 6 e Tabela 7 são apresentadas as correlações e o valor de R quadrado entre as características físicas e os parâmetros das equações que descrevem o comportamento reológico dos materiais, para as amostras com material de origem ouro e zinco, respectivamente.
| Correlação de Pearson | R quadrado | |||||||||||
| ρs | D80 | D60 | D50 | D30 | D10 | ρs | D80 | D60 | D50 | D30 | D10 | |
| α1 | 0,77 | -0,46 | -0,12 | 0,09 | 0,26 | 0,24 | 0,59 | 0,21 | 0,01 | 0,01 | 0,07 | 0,06 |
| β1 | -0,33 | 0,60 | 0,46 | 0,29 | 0,02 | 0,23 | 0,11 | 0,36 | 0,21 | 0,08 | 0,00 | 0,05 |
| α2 | 0,21 | 0,14 | 0,36 | 0,43 | 0,41 | 0,43 | 0,04 | 0,02 | 0,13 | 0,18 | 0,16 | 0,18 |
| β2 | 0,92 | -0,74 | -0,63 | -0,54 | -0,45 | -0,29 | 0,85 | 0,55 | 0,40 | 0,29 | 0,20 | 0,09 |
| Correlação de Pearson | R quadrado | |||||||||||
| ρs | D80 | D60 | D50 | D30 | D10 | ρs | D80 | D60 | D50 | D30 | D10 | |
| α1 | 0,8 | -0,34 | -0,31 | -0,31 | -0,41 | -0,39 | 0,64 | 0,11 | 0,1 | 0,1 | 0,17 | 0,16 |
| β1 | -0,12 | -0,58 | -0,65 | -0,64 | -0,53 | -0,16 | 0,02 | 0,34 | 0,42 | 0,41 | 0,28 | 0,03 |
| α2 | 0,6 | -0,22 | -0,28 | -0,27 | -0,24 | 0,05 | 0,36 | 0,05 | 0,08 | 0,07 | 0,06 | 0 |
| β2 | -0,18 | -0,45 | -0,44 | -0,43 | -0,35 | 0,18 | 0,03 | 0,2 | 0,2 | 0,19 | 0,12 | 0,03 |
Ao analisar os dados, é possível observar correlações entre a densidade dos sólidos e os parâmetros reológicos, principalmente para os valores de α1 e β2 para as amostras de ouro, e α1 para as amostras de zinco. Essa relação é particularmente explícita para a barragem 2 de ouro, ao comparar o comportamento apresentado nas Figura 1 e Figura 2 e as densidades obtidas.
Por outro lado, ainda que exista correlação entre os diâmetros e os parâmetros reológicos, em geral negativa, os valores de R quadrado indicam que a proporção da variância total da variável dependente Y, que é explicada pelo modelo de regressão, é baixa.
Na Tabela 8 e Tabela 9 são apresentados os resultados de R múltiplo, R-quadrado, R-quadrado ajustado para indicar a qualidade do ajuste da regressão para as amostras, e dos coeficientes do modelo, sendo apresentadas apenas as regressões com nível de significância inferior a 0,05.
| Variáveis | R múltiplo | R-quadrado | R-quadrado ajustado | Coeficientes | |||||
| α1 | β2 | α1 | β2 | α1 | β2 | Interseção | D1 | D2 | |
| D80 D50 | 0,94 | – | 0,88 | 0,84 | 0,0189 | -0,0007 | 0,0012 | ||
| D80 D30 | 0,83 | – | 0,69 | 0,59 | 0,0135 | -0,0004 | 0,0019 | ||
| D80 D10 | 0,93 | 0,86 | 0,82 | -0,0039 | -0,0006 | 0,0163 | |||
| 0,81 | 0,65 | 0,54 | 24,1045 | -0,1262 | 1,7586 | ||||
| D60 D10 | 0,80 | 0,64 | 0,52 | -0,0232 | -0,0012 | 0,0253 | |||
| 0,88 | 0,78 | 0,71 | 18,5182 | -0,3491 | 5,2801 | ||||
| D50 D10 | – | 0,92 | – | 0,85 | – | 0,80 | 12,4534 | -0,6933 | 9,5924 |
| Variáveis | R múltiplo | R-Quadrado | R-quadrado ajustado | Coeficientes | ||
| β1 | Interseção | D50 | D30 | |||
| D50 D30 | 0,99 | 0,98 | 0,96 | 22,5000 | -2,9087 | 9,3546 |
Para as amostras de ouro, é possível ver a influência da granulometria no comportamento reológico. Apesar de um único diâmetro não explicar bem os parâmetros reológicos, essa análise é melhorada ao incorporar diferentes diâmetros. Pelos coeficientes da regressão, tem-se relação negativa para diâmetros maiores e relação positiva para diâmetros menores, indicando que o aumento das partículas causa redução dos valores de parâmetros reológicos, como também analisado por Wang et al. (2018).
Para o zinco, a única regressão encontrada que foi aceita no teste de significância relacionou os diâmetros D50 e D30 com o coeficiente β1. Também nesse caso, o coeficiente do diâmetro maior foi negativo, enquanto o do diâmetro menor foi negativo. Entretanto, é importante ter cautela ao analisar os dados de zinco, em função do pequeno número de amostras e da diferença de comportamento notável entre resíduo e rejeito de zinco.
Em todos os casos apresentados, os valores de R, indicando o ajuste da regressão, foram considerados satisfatórios, principalmente em comparação à regressão simples.
CONSIDERAÇÕES FINAIS E RECOMENDAÇÕES
O estudo buscou entender a influência de características físicas no comportamento reológico de sedimentos, rejeitos e resíduo de mineração. Para isso, foram analisadas a granulometria, a densidade dos sólidos e os coeficientes α e β que caracterizam as curvas reológicas de tensão de cisalhamento em função de CV e viscosidade dinâmica em função de CV das 22 amostras de diferentes materiais oriundos do beneficiamento de zinco, bauxita e ouro, e sedimentos de uma bacia antropizada.
Para além disso, buscou-se por correlação e regressão. Entendendo a influência do material de origem, essas análises foram feitas para as amostras de zinco e ouro, por apresentarem mais dados. Em uma correlação linear, observaram-se indícios nas amostras de que o aumento dos valores de densidade dos sólidos leva a valores maiores dos parâmetros α1 e β2, para ouro, e α1, para o zinco. Em seguida, por meio da regressão linear múltipla, foi observado que o aumento dos diâmetros está relacionado à redução dos valores de α1 e β2, para ouro e de β1, para zinco. Observou-se também um ganho ao utilizar a regressão linear múltipla, indicando que não só o diâmetro característico importa, e sim a granulometria mais bem caracterizada, evidenciando a complexidade do comportamento reológico.
Destaca-se que foram encontrados indícios de relações entre as características físicas e o comportamento reológico, entretanto a análise não é conclusiva em função do baixo número de dados. Dessa forma, sugere-se a continuidade do estudo, no sentido de agregar mais amostras. Além disso, é sugerida que sejam consideradas a mineralogia, formato dos grãos, processo produtivo e outras características dos materiais, além de análises não lineares, de forma a trazer mais robustez à análise.
Por fim, salienta-se que os parâmetros alcançados a partir das amostras avaliadas estão coerentes com aqueles observados na literatura.
ADIGUZEL, D; BASCETIN, A. (2019). The investigation of effect of particle size distribution on flow behavior of paste tailings. Journal of environmental management, v. 243, p. 393-401.
BINGHAM, E.C. (1922). Fluidity and plasticity, McGraw-Hill, New York, 439.
CHIEN, N.; MA, H. (1958), ‘Properties of slurry flow’, J. Sediment Res. 3(3).
DAI, J. (1980), An experimental study of slurry transport in pipes, in ‘Proc, Int. Symposium on River Sedimentation’, China., pp. 195–204.
DESRIVIERS, P.; QUINTERO, A.; PRIMEAU, P. (2019), ‘Effects of the mineralogical composition and particle size distribution on the rheology of gold and copper tailings’, in AJC Paterson, AB Fourie & D Reid (eds), Paste 2019: Proceedings of the 22nd International Conference on Paste, Thickened and Filtered Tailings, Australian Centre for Geomechanics, Perth, pp. 504-514.
FEI, X. J. (1981). Bingham yield stress of sediment water mixtures with hyperconcentration. J. Sediment Res. 3.
KANG, Z. e ZHANG, S. (1980), A preliminary analysis of the characteristics of debris flow., in ‘Proc, Int. Symposium on River Sedimentation’, China., pp. 213–220.
LIDA, K. (1938), ‘The mud flow that occurred near the explosion crater of mt. bandai on may 9 and 15, 1938, and some physical properties of volcanic mud’, Tokyo Imperial University Earth- quake Research Institute Bulletin 16.
NAGHETTINI, M; PINTO, E, J. de A. (2007). Hidrologia estatística. Belo Horizonte: CPRM.
O’BRIEN, J. S.; JULIEN, P. Y. (1988). “Laboratory analysis of mudflow properties”. J. Hydraul. Eng., 114, 877–887.
QIAN, N. (1980), Basic characteristics of flow with hyperconcentration of sediment, in ‘Proc, Int. Symposium on River Sedimentation’, China., pp. 175–184.
WANG, X.; WEI, Z.; LI, Q. (2018), ‘Experimental research on the rheological properties of tailings and its effect factors’. Environ Sci Pollut Res 25, 35738–35747 (2018). https://doi.org/10.1007/s11356-018-3481-1.
ZENGENI, B. T. (2016), ‘Bingham Yield Stress and Bingham Plastic Viscosity of Homogeneous Non-Newtonian Slurries’. Bellville, Western Cape, South Africa: Cape Peninsula University of Technology.
1 HIDROBR Consultoria LTDA., Av. Brasil, nº 888, 14º andar, Belo Horizonte, Brasil, (31) 99726-1113, vitor.lages@hidrobr.com.
2 HIDROBR Consultoria LTDA., Av. Brasil, nº 888, 14º andar, Belo Horizonte, Brasil, (31) 99771-9513, victoria.braga@hidrobr.com.
3 HIDROBR Consultoria LTDA., Av. Brasil, nº 888, 14º andar, Belo Horizonte, Brasil, (31) 98654-8028, clara.demattos@hidrobr.com.
4 HIDROBR Consultoria LTDA., Av. Brasil, nº 888, 14º andar, Belo Horizonte, Brasil, (31) 9.9591-8383, mariana.almeida@hidrobr.com.
5 HIDROBR Consultoria LTDA., Av. Brasil, nº 888, 14º andar, Belo Horizonte, Brasil, (98) 99124-2427, malena.melo@hidrobr.com.
Acompanhe nossas novidades e oportunidades pelo Linkedin